Walkway Discovery - carlhruska.com

I suppose I could have titled this article as Secret of Sidewalk Revealed or Walkway Wonder Discovered, but I’m just calling it Walkway Discovery.

Warning – This is a little journey into Math Land.

I went to the local park one day in April 2022 to meet my friend for a walk.

While I waited, I noticed the pattern of the walkway. That is, the way each section of cement was next to an adjacent section, visibly separated by a strip of wood or a thin trowel line. The walkway itself is an inner sidewalk around the large, central area of the park that people use for sports’ games, dog walking, kite flying, and other relaxing activities.

The walkway begins perpendicularly at the edge of the sidewalk and extends a few feet into the park area. At that point, it branches both left and right (thereby being parallel with the sidewalk as the walkway continues around the inside of the park).

Note: to enlarge any picture, right-click the picture and then select the option labeled “Open image in new tab”. Click the new tab to see the larger picture.

Dismiss the new tab/picture by clicking its X.

Visualize (above), if you will, two walking paths (one next to the street and another further from the street), parallel with each other and separated from each other by about eight feet.

Now, the location of the walkway that I wish to focus on is one of the places where the perpendicular part of the walkway turns into a parallel part. That part of the cement walkway is gently curved (as opposed to making a sharp, ninety-degree angle).

I looked at that curve and visualized it as being part of the circumference of a circle (an arc) (if I were to extend the arc to form a full circle).

I defined in my mind the ends of the arc as the two places where the curved parts begin extending as straight lines.

I further visualized a straight line between (“connecting”) the two ends of the arc, making a figure like the cornea of the human eye or a convex lens.

I wondered if the area of that figure could be determined.

I suppose my dealing with math all of my life made me think about this.

At any rate, I started to wonder if a formula had been devised to calculate an area of a figure having a perimeter composed of both a curved line and a straight-line.

My first thought was that calculus would be needed (dealing with curves in this case). I had revisited that subject some months ago but did not want to go there again. Who would? There must be another way. But I couldn’t think of any other way.

So, to the internet I go.

I searched for “section of a circle”, but the formula I found did not apply in this case.

I searched some more and luckily stumbled upon the formula I needed. The area in this particular situation is called a SEGMENT.

How surprising (to me)! Some very smart person (no telling how many years ago) devised the formula to calculate the area of a figure made up of a straight line and a curved line.

[If the angle is in radians, the formula for the area is 1/2 * r² * (θ – sin(θ)]

But if the angle is in degrees, the formula is just slightly more complicated. It is Area = 1/2 * r² * ((π/180 * θ) – sin(θ))

That is, 1/2 of the radius squared times the difference between [(π/180 times the actual angle) and (the sine of the angle)].

For example, suppose the radius is 26 units long and the angle is 90°.

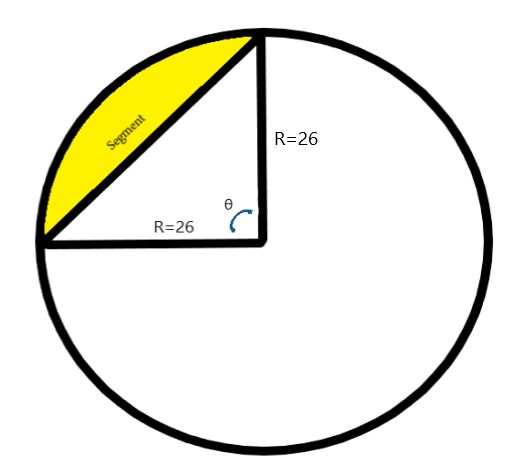
The area (with a little rounding) would be 0.5 * 26²* [(0.01745 * 90) – (sin(90)]

That is, 0.5 * 676 * (1.5708 – 1),

which is 0.5 * 676 * 0.5708

Resulting in 192.93 square units (close enough for me).

Of course, I wanted to see if I had understood what I had read online.

So, I thought of an experiment to verify my understanding.

I figured that if I calculated the area of the triangle under the segment and added that “triangle-area” to the area I just calculated above for the segment, that combined value would be one-fourth of the area of the circle. Multiplying by 4 would give me the area of the whole circle. That answer I would call Answer1.

I could then compare that Answer1 with the area of the circle calculated by the standard formula we all learned back in school: area = π r². This would be Answer2.

So, area of triangle = ½ X base X height = ½ X 26 X 26 = 338

Area of one-fourth of the circle is 338 + 192.93 = 530.93

Area of the full circle (Answer1) is 4 X 530.93 = 2123.7 (rounded gives 2124).

Answer2 = 3.1415 X 26²= 3.1415 X 676 = 2124.

SUCCESS! (And relief)

But wait a minute! Does the formula work for any angle?

To find out, I experimented with an angle of 45°.

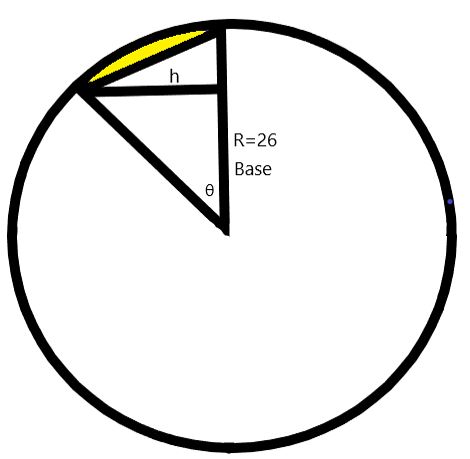
Repeating the formula for the area of the segment: 1/2 * r² * ((π/180 * θ) – sin(θ))

So, the area of the segment is 0.5 * 26²* [(0.01745 * 45) – (sin(45)]

That is, 0.5 * 676 * (.78525 – .707),

which is 0.5 * 676 * .07825

Resulting in 26.448 (the area of the segment)

Now, to get the area of the triangle under the segment, we need the height of the triangle, because the formula for the area of a triangle is ½ * Base * Height.

Notice that the length of the base is the same as the length of the hypotenuse.

The sine of 45° is defined as the length of the opposite side (labeled as “h”) divided by the length of the hypotenuse (the radius). That is, sin(45) = h / radius. Which is the same as sin(45) * radius = h.

So, h = sin(45°) * 26

Or h = .707 * 26

Or h = 18.382 (this is the height).

So, the area of the triangle is ½ * 26 * 18.382 = 238.966.

Adding the area of the segment (26.448) to the area of the triangle (238.966) gives 265.414.

This combined area is 1/8 the area of the entire circle.

So, 8 * 265.414 = 2123. Except for rounding errors, both answers (for 90° and 45°) are the same, proving (to me, at least) that the formula works for any angle.

This involvement with some math was actually kind of fun. What did he say??? I enjoyed going back to some math basics during my research, but actually, I would not like to do it everyday (even if someone paid me, let’s say, $100/hour minimum, thank you).